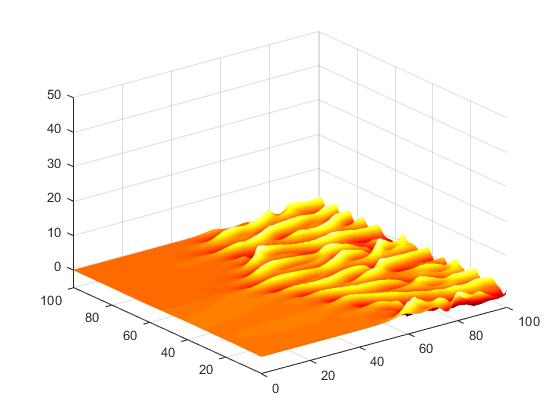
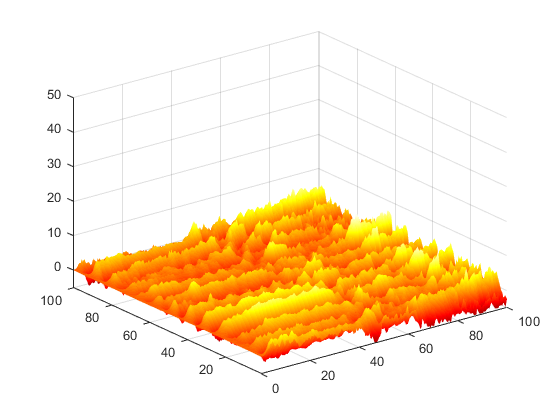
I used neural networks to determine time stepping evolution of dynamic systems given an initial condition. I trained the neural networks with differential equations solved with MATLAB’s ode45 solver for multiple random initial conditions.

The full paper describing this project is here.

Neural Networks are a useful tool for determining the evolution of dynamic systems based on a set of training trajectories and then providing the neural network with an initial condition. For this exercise, we used known differential equations which we solved with numerical tools to compare the performance of neural network models. In general, neural networks are useful to model dynamics for systems in which the governing equations are unknown and actual measurements are the only way to compare a model to a dynamic system.

The systems include a lambda-omega reaction-diffusion (RD) system, a Kuramoto-Sivashinsky (KS) system, and a Lorenz system.